|
(1)
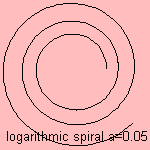
Logarithmic spiral is the spiral for which the radius grows exponentially with the angle. The logarithmic relation between radius
and angle leads to the name of logarithmic spiral or logistique (in French).
The distances where a radius from the origin meets the curve are in geometric progression.
The curve was the favorite of Jakob (I) Bernoulli (1654-1705). On his request his tombstone, in the Munster
church in Basel, was decorated with a logarithmic spiral. The curve, which looks by the way more like
an Archimedes' spiral, has the following Latin text accompanied: eadem mutata resurgo. In a free
translation: 'although changed, still remaining the same'. This refers to the various operations for which the
curve remains intact (see below).
Therefore the curve is also called the Bernoulli spiral.
 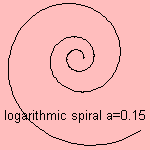  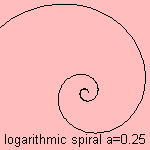
However, Rene Descartes (1638) was the first to study the curve. Torricelli worked on the curve independently,
and found the curve's length.
The curve is also named to Fibonacci as the Fibonacci spiral.
(2)
An Archimedean spiral (also arithmetic spiral), is a spiral named after the 3rd-century-BC Greek mathematician
Archimedes; it is the locus of points corresponding to the locations over time of a point moving away from a fixed
point with a constant speed along a line which rotates with constant angular velocity. Equivalently, in polar
coordinates (r, θ) it can be described by the equation
r = a + b·θ
with real numbers a and b. Changing the parameter a will
turn the spiral, while b controls the distance between successive turnings.
Archimedes described such a spiral in his book On Spirals.
This Archimedean spiral is distinguished from the logarithmic spiral by the fact that successive turnings of
the spiral have a constant separation distance (equal to 2πb if θ is measured in radians), while in a
logarithmic spiral these distances form a geometric progression.
Note that the Archimedean spiral has two arms, one for θ > 0 and one for θ < 0. The two arms are smoothly connected
at the origin. Only one arm is shown on the accompanying graph. Taking the mirror image of this arm across
the y-axis will yield the other arm.
One method of squaring the circle, by relaxing the strict limitations on the use of straightedge and compass in
ancient Greek geometric proofs, makes use of an Archimedean spiral.
Sometimes the term Archimedean spiral is used for the more general group of spirals
r = a + b·θ1/x
The normal Archimedean spiral occurs when x = 1. Other spirals falling into this group include the hyperbolic spiral,
Fermat's spiral, and the lituus. Virtually all static spirals appearing in nature are logarithmic spirals, not
Archimedean ones. Many dynamic spirals (such as the Parker spiral of the solar wind, or the pattern made by a
Catherine's wheel) are Archimedean.
|